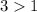Answer:
A.
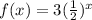
Explanation:
The options are:
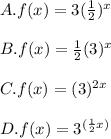
For this exercise it is important to remember that, by definition, the Exponential parent functions have the form shown below:
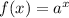
Where "a" is the base.
There are several transformations for a function f(x), some of those transformations are shown below:
1. If
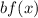 and
and
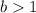 , then the function is stretched vertically by a factor of "b".
, then the function is stretched vertically by a factor of "b".
2. If
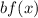 and
and
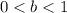 , then the function is compressed vertically by a factor of "b"
, then the function is compressed vertically by a factor of "b"
Therefore, based on the information given above, you can identify that the function that represents a vertical stretch of an Exponential function, is the one given in the Option A. This is:
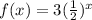
Where the factor is:
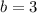
And