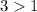Question

Which function represents a vertical stretch of an exponential function?

-
Rx)=3()
F(x) = 1 / (3) *
F(x) = (3) 2x

Answer 1

A.

Explanation:

Answer 2

A.
`f(x)=3((1)/(2))^x`

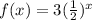
Explanation:

The options are:

`A. f(x)=3((1)/(2))^x\\\\B. f(x)=(1)/(2)(3)^x\\\\C. f(x)=(3)^(2x)\\\\ D. f(x)=3^{((1)/(2)x)}`

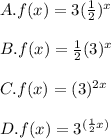
For this exercise it is important to remember that, by definition, the Exponential parent functions have the form shown below:

`f(x) = a^x`

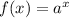
Where "a" is the base.

There are several transformations for a function f(x), some of those transformations are shown below:

1. If
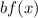`bf(x)` and
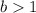`b>1`, then the function is stretched vertically by a factor of "b".

2. If
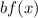`bf(x)` and
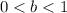`0<b<1`, then the function is compressed vertically by a factor of "b"

Therefore, based on the information given above, you can identify that the function that represents a vertical stretch of an Exponential function, is the one given in the Option A. This is:

`f(x)=3((1)/(2))^x`

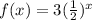
Where the factor is:

`b=3`

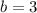
And
`3>1`