Question

15. The legs of a right triangle measure 3

and 5, respectively. Determine whether
the side lengths form a Pythagorean
triple and, if not, why not.​

Answer 1

The right triangle of sides 3 and 5 does not form Pythagorean triple.

Step-by-step explanation:

A Pythagorean triple is a triple of positive integers a, b, and c such that a right triangle exists with legs a,b and hypotenuse c. By the Pythagorean theorem, this is equivalent to finding positive integers a, b, and c satisfying

`a^2+b^2=c^2.`

The smallest and best-known Pythagorean triple is (a,b,c)=(3,4,5). The right triangle having these side lengths is sometimes called the 3, 4, 5 triangle.

Here in the question the legs of the right triangle are 3 and 5

Now by using Pythagorean theorem

`3^2+5^2 = c^2`

`9+25 = c^2`

`34 = c^2`

`c= √(34)`

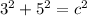
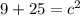
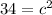
Hence it is not a Pythagorean triple