Answer:
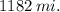
Step-by-step explanation:
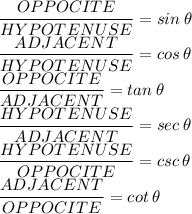
You are travelling from one location to another at a directional angle of 100°. So, we will use the cosecant trigonometric ratio to determine how far west the aeroplane travelled to its destination:

I am joyous to assist you at any time.