Answer:
The expected wining from 1 ticket will be −41 cents.
Explanation:
Consider the provided information.
A raffle offers a first prize of $1000, 2 second prizes of $300, and 20 third prizes of $10 each.
Out of 20000 tickets the probability of not winning is:
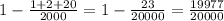
The expected value of gain or loss is:
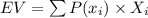
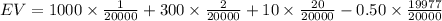
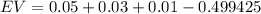
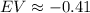
The expected wining from 1 ticket will be −41 cents.