Question

Use your understanding of the symmetry of the sine and cosine functions to determine the value of tan(−theta) for all

real-numbered values of theta. Determine whether the tangent function is even, odd, or neither.

Answer 1

`tan(-\theta)=-tan\theta`

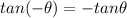
Odd function

Explanation:

We are given that

`tan(-\theta)`

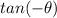
We have to determine the value of
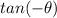`tan(-\theta)`and find tangent function is odd,even or neither.

`tan(-\theta)=(sin(-\theta))/(cos(-\theta))`

`tan\theta=(sin\theta)/(cos\theta)`

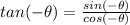
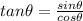
We know that

`sin(-\theta)=-sin\theta`

`cos(-\theta)=cos\theta`

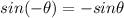
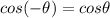
By using identities

Then, we get

`tan(-\theta)=(-sin\theta)/(cos\theta)=-tan\theta`

`tan(-\theta)=-tan\theta`

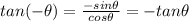
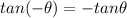
Odd function: If
`f(-x)=-f(x)`

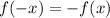
Even function:If
`f(-x)=f(x)`

`tan(-\theta)=-tan\theta`

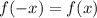
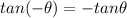
Therefore, function is an odd function.