Answer:
a)
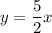
b) yes the two lines are perpendicular
c)
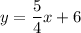
Explanation:
a) All this is asking if to find a line that is perpendicular to 2x + 5y = 7 AND passes through the origin.
so first we'll find the gradient(or slope) of 2x + 5y = 7, this can be done by simply rearranging this equation to the form
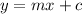

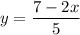
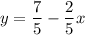
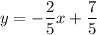
this is changed into the
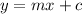 , and we easily see that -2/5 is in the place of m, hence
, and we easily see that -2/5 is in the place of m, hence
 is the slope of the line 2x + 5y = 7.
is the slope of the line 2x + 5y = 7.
Now, we need to find the slope of its perpendicular. We'll use:
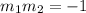 .
.
here both slopes
 and
and
 are slopes that are perpendicular to each other, so by plugging the value -2/5 we'll find its perpendicular!
are slopes that are perpendicular to each other, so by plugging the value -2/5 we'll find its perpendicular!
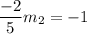 .
.
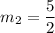 .
.
Finally, we can find the equation of the line of the perpendicular using:
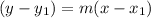
we know that the line passes through origin(0,0) and its slope is 5/2
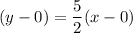
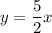 is the equation of the the line!
is the equation of the the line!
b) For this we need to find the slopes of both lines and see whether their product equals -1?
mathematically, we need to see whether
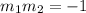 ?
?
the slopes can be easily found through rearranging both equations to
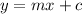
Line:1
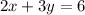
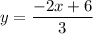
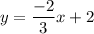
Line:2
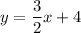
this equation is already in the form we need.
the slopes of both equations are
 and
and
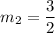
using
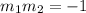
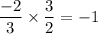
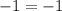
since the product does equal -1, the two lines are indeed perpendicular!
c)if two perpendicular lines have the same intercept, that also means that the two lines meet at that intercept.
we can easily find the slope of the given line, y = − 4 / 5 x + 6 to be
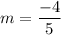 and the y-intercept is
and the y-intercept is
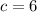 the coordinate at the y-intercept will be (0,6) since this point only lies in the y-axis.
the coordinate at the y-intercept will be (0,6) since this point only lies in the y-axis.
we'll first find the slope of the perpendicular using:
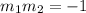
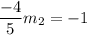
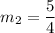
we have all the ingredients to find the equation of the line now. i.e (0,6) and m
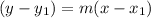
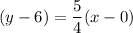
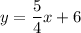
this is the equation of the second line.
side note:
this could also have been done by simply replacing the slope(m1) of the y = − 4 / 5 x + 6 by the slope of the perpendicular(m2): y = 5 / 4 x + 6