The areas of the two watch faces have a ratio of 16:25 What is the ratio of the radius of the smaller watch face to the radius of the larger watch face?

Question

asked Oct 25, 2021 160k views

1 Answer

Megabri · Answer 1 · 2021-10-31T22:07:44+0000

Answer:

The ratio of the radius of the smaller watch face to the radius of the larger watch face is 4:5.

Explanation:

Let the Area of smaller watch face be

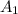
Also Let the Area of Larger watch face be

Also Let the radius of smaller watch face be

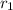
Also Let the radius of Larger watch face be

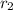
Now given:

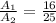
(A_1)/(A_2) =(16)/(25)

We need to find the ratio of the radius of the smaller watch face to the radius of the larger watch face.

Solution:

Since the watch face is in circular form.

Then we can say that;

Area of the circle is equal 'π' times square of the radius 'r'.

framing in equation form we get;

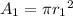
$A_1 = \pi {r_1}^2$

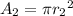
$A_2 = \pi {r_2}^2$

So we get;

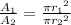
$(A_1)/(A_2)= \frac{\pi {r_1}^2}{\pi {r_2}^2}$

Substituting the value we get;

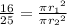
$(16)/(25)= \frac{\pi {r_1}^2}{\pi {r_2}^2}$

Now 'π' from numerator and denominator gets cancelled.

$(16)/(25)= \frac{{r_1}^2}{{r_2}^2}$

Now Taking square roots on both side we get;

$\sqrt{(16)/(25)}= \sqrt{\frac{{r_1}^2}{{r_2}^2}}\\\\(4)/(5)= (r_1)/(r_2)$

Hence the ratio of the radius of the smaller watch face to the radius of the larger watch face is 4:5.