Question

1. Different students drew random samples of size 50 from the mystery bag. The number of red chips each drew is given below. In each case, find the margin of error for the proportions

of the red chips in the mystery bag.
a. 10 red chips
b. 28 red chips
c. 40 red chips

Answer 1

Part A:

Margin of error=M≅0.1131

Part B:

Margin of error=M≅0.1404

Part C:

Margin of error=M≅0.1131

Explanation:

The formula for finding the margin of error for the proportion is:

Margin of error=M=
`2*\sqrt{(p(1-p))/(n) }`

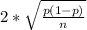
where:

p is the sample proportion =
`(Number of Chips)/(Samlpe Size)`

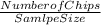
n is the sample size

Part A:

Margin of error=M=
`2*\sqrt{(p(1-p))/(n) }`

p=
`(10)/(50)`

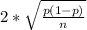
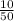
p=0.2

Margin of error=M=
`2*\sqrt{(0.2*(1-0.2))/(50)}`

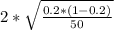
Margin of error=M≅0.1131

Part B:

p=
`(28)/(50)`

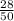
p=0.56

Margin of error=M=
`2*\sqrt{(0.56*(1-0.56))/(50)}`

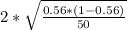
Margin of error=M≅0.1404

Part C:

p=
`(40)/(50)`

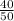
p=0.8

Margin of error=M=
`2*\sqrt{(0.8*(1-0.8))/(50)}`

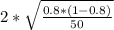
Margin of error=M≅0.1131