Question

1. Consider a right triangle drawn on a page with sides of lengths 3 cm, 4 cm, and 5 cm.

a. Describe a sequence of straightedge and compass constructions that allow you to draw the circle that circumscribes the triangle. Explain why your construction steps successfully
accomplish this task.
b. What is the distance of the side of the right triangle of length 3 cm from the center of the circle that
circumscribes the triangle?
c. What is the area of the inscribed circle for the triangle?

Answer 1

a)

1. First we need to draw a perpendicular bisector of the side AB.
2. Next, draw a perpendicular bisector of the side BC. We use the same method above.
3. Now, put 0 where the bisectors intersect.
4. Finally, put one part of the compass on 0 an the other part on C and draw the circle.

b)
`x=2.9 cm`

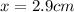
c) R = 1 cm.

Explanation:

Let's define:

AB: distance of the side with length 3 cm

AC: distance of the side with length 4 cm

BC: distance of the side with length 5 cm

a)

1. First we need to draw a perpendicular bisector of the side AB. We just put he compass in A, with any distance and trace two semicircle between AB.
2. Next, draw a perpendicular bisector of the side BC. We use the same method above.
3. Now, put 0 where the bisectors intersect.
4. Finally, put one part of the compass on 0 an the other part on C and draw the circle.

b)

In a right triangle the hypotenuse of the triangle is the diameter of its circumscribe circle, so the radius of the circle is equal to half of the hypotenuse of the right triangle.

So if we draw a line from the center to the middle of the AB we will have new triangle, with sides BC/2, AB/2 and x, when x is the distance from the center to the length 3 cm. Therefore x will be:

`x=\sqrt{(5/2)^(2)+(3/2)^(2)}=2.9 cm`

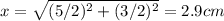
c)

We need to find the radius of the circle to find the area.

So we can use this formula.

`A=(P\cdot R)/(2)`

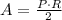
A is the triangle area, it is AC*AB/2 = 6 cm²

P is the triangle perimeter, it is AC+AB+BC = 12 cm

R is the radius of the inner circle.

Then, R = 2*6/12 = 1 cm.

Have a nice day!

Answer 2

Answer: circumcircle is a circle that passes through the three edges(vertices) of the triangle

Step-by-step explanation: constuction:

in the triangle labelled xyz,choose any two sides, say, xy and xz.construct the perpendicular bisector of the two sides xz and xy to meet at P.

Using P as the center and radius equal to PX, draw a circle which will pass through the edges of X,Y, z. the required circle is the circumcircle.