Answer:
The possible co-ordinates of the point Q are (0,5) and (0,17).
Explanation:
Given:
P is a point (8,11)
Q is point on y-axis
PQ = 10 units
To find co-ordinates of point Q.
Solution:
Any point on y-axis is given as
 as
as
 at y-axis.
at y-axis.
Let the point Q be =

We use the distance formula to find length of PQ.
By distance formula:
The distance between two points
 and
and
 is given as:
is given as:
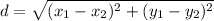
Thus, for the point P(8,11) and Q(0,
 ) the distance PQ can be given as:
) the distance PQ can be given as:
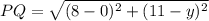
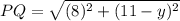
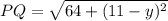
Substituting PQ=10 units.
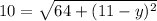
Squaring both sides.
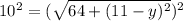
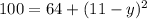
Subtracting both sides by 64.

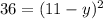
Taking square root both sides.

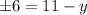
So, we have two equations to solve:
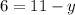 and
and
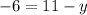
Adding
 both sides.
both sides.
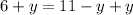 and
and
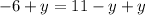
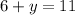 and
and
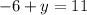
Subtracting both sides by 6 for one equation and adding 6 both sides for the other equation.
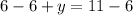 and
and
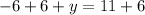
∴
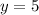 and
and
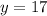
Thus, the possible co-ordinates of the point Q are (0,5) and (0,17).