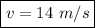Question

A 75.5 kg diver drops from a diving board 10.0 m above the waters surface. Find the divers speed just before he strikes the water.

Answer 1

v=14 m/s

Step-by-step explanation:

Mechanical Energy

The kinetic energy of a body (K) is the capacity of doing work due to its speed. It can be expressed as

`\displaystyle K=(mv^2)/(2)`

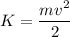
The potential energy (U) is the capacity of doing work due to its height respect to a certain reference level.

`U=mgh`

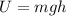
The mechanical energy is the sum of both

`\displaystyle E_m=(mv^2)/(2)+mgh`

The principle of conservation of mechanical energy states it must remain the same if no external force is acting on it. The diver drops from the diving board, which means its initial speed is zero (and so its initial kinetic energy). Thus, the mechanical energy at the jumping time is

`\displaystyle E_m=mgh=(75)(10)(9.8)=7350\ J`

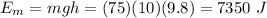
When the diver is about to get into the water, his height reaches zero and the speed is at maximum. All the potential energy became kinetic energy, so

`\displaystyle (mv^2)/(2)=7350\ J`

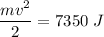
Rearranging

`\displaystyle v^2=(2(7350))/(75)=196`

`v=√(196)=14\ m/s`

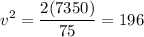
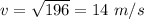
The final speed of the diver is

`\boxed{v=14\ m/s}`