Question

1. Given points ????(3, −5) and ????(19, −1), find the coordinates of point ???? that sit 3/8 of the way along AB ,close to A than to B.

Answer 1

Answer: The required co-ordinates of point C are (9, -3.5).

Step-by-step explanation: We are given the points A(3, -5) and B(19, -1).

We are to find the co-ordinates of point C that sit 3/8 of the way along AB, where the point P is close to A than to B.

According to the given information, we have

`(AC)/(AB)=(3)/(8)\\\\\Rightarrow (AC)/(AC+BC)=(3)/(8)\\\\\Rightarrow 8AC=3AC+3BC\\\\\Rightarrow 5AC=3BC\\\\\Rightarrow AC:BC=3:5.`

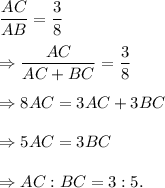
So, point C divides the line segment AB in the ratio 3 : 5.

We know that

if a point Q divides a line segment joining the points S(a,b) and T(c,d), in the ratio m : n, then the co-ordinates of Q are

`\left((mc+na)/(m+n),(md+nb)/(m+n)\right).`

Therefore, the co-ordinates of point C are

`\left((3*19+5*3)/(3+5),(3*(-1)+5*(-5))/(3+5)\right)\\\\\\=\left((57+15)/(8),(-3-25)/(8)\right)\\\\=(9,-3.5).`

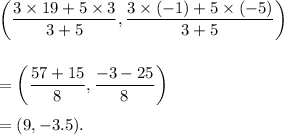
Thus, the required co-ordinates of point C are (9, -3.5).