Question

10. Divide the problems below among your group, and find the sample proportion of successes and the estimated margin of error in each situation:

a. Sample of size 20, 5 red chips
b. Sample of size 40, 10 red chips
c. Sample of size 80, 20 red chips
d. Sample of size 100, 25 red chips

Answer 1

a) 0.1936

b) 0.137

c) 0.097

d) 0.087

Explanation:

Margin of error is given as:

E =
`2\sqrt{(p(1-p))/(n)}`

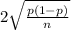
here,

p is the probability of event

n is the sample size

a. Sample of size 20, 5 red chips

n = 20

p = 5 ÷ 20

= 0.25

Thus,

E =
`2\sqrt{(0.25(1-0.25))/(20)}`

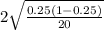
or

E = 0.1936

b. Sample of size 40, 10 red chips

n = 40

p = 10 ÷ 40

= 0.25

Thus,

E =
`2\sqrt{(0.25(1-0.25))/(40)}`

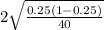
or

E = 0.137

c. Sample of size 80, 20 red chips

n = 80

p = 20 ÷ 80

= 0.25

Thus,

E =
`2\sqrt{(0.25(1-0.25))/(80)}`

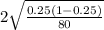
or

E = 0.097

d. Sample of size 100, 25 red chips

n = 100

p = 25 ÷ 100

= 0.25

Thus,

E =
`2\sqrt{(0.25(1-0.25))/(100)}`

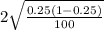
or

E = 0.087