Answer:
Therefore,
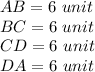
Since , ABCD has four Right angles and four Congruent sides, it is a Square
Explanation:
The four points for the Figure are
point A( x₁ , y₁) ≡ ( 0 , 6)
point B( x₂ , y₂) ≡ (6 , 6)
point C(x₃ , y₃ ) ≡ (6 , 0)
point D(x₄ , y₄ ) ≡ (0 , 0)
∠A = ∠B = ∠C = ∠D = 90°
To Prove:
ABCD is a Square
Proof:
∠A = ∠B = ∠C = ∠D = 90° .........Given:
Now By Distance Formula we have
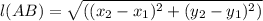
Substituting we get
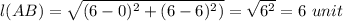
Similarly for BC ,CD ,DA we have



Therefore,
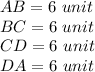
Since , ABCD has four Right angles and four Congruent sides, it is a Square