Question

A 50.0-g hard-boiled egg moves on the end of a spring with force constant k = 25.0 N/m. It is released with an amplitude 0.300 m. A damping force F_x = -bv acts on the egg. After it oscillates for 5.00 s, the amplitude of the motion has decreased to 0.100 m.Calculate the magnitude of the damping coefficient b.Express the magnitude of the damping coefficient numerically in kilograms per second, to three significant figures.

Answer 1

given,

mass of the boiled egg = 50 g = 0.05 Kg

spring constant, k = 25 N/m

initial Amplitude, A₁ = 0.3 m

final amplitude, A₂ = 0.1 m

time, t = 5 s

considering the amplitude of damped harmonic oscillation to calculate damping factor.

`A_2 = A_1 e^{-((b)/(2m))t}`

b is the damping factor and t is the time.

`e^{-((b)/(2m))t}=(A_2)/(A_1)`

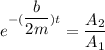
on solving

`b= (2m)/(t)ln((A_1)/(A_2))`

inserting all the given values

`b= (2* 0.05)/(5)ln((0.3)/(0.1))`

b = 0.0219 Kg/s

damping coefficient in three significant figure

b = 0.022 Kg/s