Question

The distribution constant for a molecule X between n-hexane and water

is 13.5. Calculate the percent of X remaining in the water phase that
was originally 0.0100 M in Z after extraction of 50.0 mL of water with
4 extractions of 10.0 mL portions of n-hexane.

Answer 1

X = 0.005%

Step-by-step explanation:

The concentration of X remaining in the water phase can be calculated using the next equation:

`[X]_(i) = ((V_(aq))/(V_(or)KD + V_(aq)))^(i) \cdot [X_(0)]`

Where:

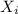`X_(i)`: is the concentration of A remaining in aqueous solution

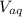`V_(aq)`: is the volume of water

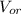`V_(or)`: is the volume of the organic solvent

KD: is the distribution constant of X between water and the organic solvent

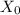`X_(0)`: is the original concentration of X

i: is the number of extractions with the organic solvent

`[X]_(i) = ((50 mL)/(10 mL \cdot 13.5 + 50 mL))^(4) \cdot 0.01 M = 5.34 \cdot 10^(-5) M`

The percent of X remaining in the water phase is:

`[X]_(i) = 5.34 \cdot 10^(-5) \cdot 100 \% = 0.005 \%`

I hope it helps you!