Answer:
The quadrilateral is not a parallelogram
Explanation:
we know that
In a parallelogram opposite sides are parallel and congruent
Find the length of the sides of the quadrilateral
step 1
Find the distance QR
the formula to calculate the distance between two points is equal to
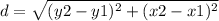
we have
Q(-10,-2), R(1,-1)
substitute
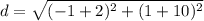
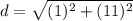
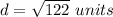
step 2
Find the distance TS
the formula to calculate the distance between two points is equal to
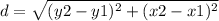
we have
T(-11,-8), S(1,-7)
substitute


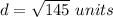
we have that
QR and TS are opposite sides
In a parallelogram opposite sides are congruent but in this problem
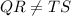
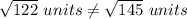
therefore
The quadrilateral is not a parallelogram