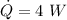Question

A cylinderical shaped metal rod is used to conduct heat.

Whenthe temperature at one end is 100 degree Celsius and at the
otherend is 20 degree Celsius, heat is transferred at a rate of 16
J/s.The rod is then stretched uniformly to twice its original
length.If again it has ends at 100 degree Celsius and 20 degree
Celsius,at what rate will heat be transferred between it
ends?

Answer 1

`\dot Q=4\ W`

Step-by-step explanation:

Given:

• temperature at one end of the rod,
  `T_1=20^(\circ)C`

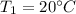
• temperature at the other end of the rod,
  `T_2=100^(\circ)C`

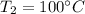
• amount of heat transferred in the first case,
  `\dot Q=16\ J.s^(-1)`

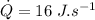
• let initial length of the rod be,
  `L`

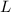
• length of the rod in second case,
  `2L`

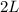
Using Fourier's law of conduction:

`\dot Q=k.A.(dT)/(L)`

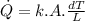
where:

k = thermal conductivity of the material

A = cross-sectional area normal to the direction of temperature change

dT = temperature difference

L = length across the surfaces of temperature difference

Now, when the rod is stretched to twice its length then its area becomes half because its volume remains constant.

Hence Fourier's law becomes:

`\dot Q=k.(A)/(2).(dT)/(2L)`

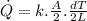
the new rate of heat transfer is

`\dot Q=4\ W`