Question

The heat of combustion of oleic

acid(C18H34O2) under
standardconditions of temperature and pressure is
-1.11x104kJ/mol. Calculate the heat of formation of
oleic acid.

Answer 1

Answer: The heat of formation of oleic acid is -94.12 kJ/mol

Step-by-step explanation:

We are given:

Heat of combustion of oleic acid =
`-1.11* 10^4kJ/mol`

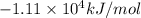
The chemical equation for the combustion of oleic acid follows:

`C_(18)H_(34)O_2(l)+(51)/(2)O_2(g)\rightarrow 18CO_2(g)+17H_2O(g);\Delta H^o=-1.11* 10^4kJ`

Enthalpy change is defined as the difference in enthalpies of all the product and the reactants each multiplied with their respective number of moles. It is represented as
`\Delta H^o`

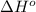
The equation used to calculate enthalpy change is of a reaction is:

`\Delta H^o_(rxn)=\sum [n* \Delta H^o_f(product)]-\sum [n* \Delta H^o_f(reactant)]`

The equation for the enthalpy change of the above reaction is:

`\Delta H^o_(rxn)=[(18* \Delta H^o_f_((CO_2(g))))+(17* \Delta H^o_f_((H_2O)))]-[(1* \Delta H^o_f_{(C_(18)H_(34)O_2(l))})+((51)/(2)* \Delta H^o_f_((O_2(g))))]`

We are given:

`\Delta H^o_f_((CO_2(g)))=-393.51kJ/mol\\\Delta H^o_f_((H_2O(g)))=-241.82kJ/mol\\\Delta H^o_f_((O_2))=0kJ/mol\\\Delta H^o_(rxn)=-1.11* 10^4kJ`

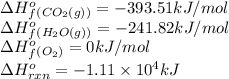
Putting values in above equation, we get:

`-1.11* 10^4=[(18* (-393.51))+(17* (-241.82))]-[(1* \Delta H^o_f_{(C_(18)H_(34)O_2(l))})+((51)/(2)* 0)]\\\\\Delta H^o_f_{(C_(18)H_(34)O_2(l))}=-94.12kJ/mol`

Hence, the heat of formation of oleic acid is -94.12 kJ/mol