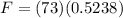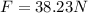Question

The water skier has a mass of 73 kg. Find the magnitude of the

netforce acting on the skier when A) she is accelerating from rest
toa speed of 11m/s in 8.0s (she is being pulled by a boat) B)
shelets go of the tow rope and glides to a halt in 21s.

Answer 1

To solve this problem we will apply the linear motion kinematic equations, specifically the concept of acceleration as a function of speed and time, as well as Newton's second law.

PART A) Acceleration can be described as changing the speed in a period of time therefore,

`a = (V)/(t)\\a = (11)/(8)\\a = 1.375m/s^2`

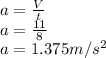
Force is the proportional change between mass and acceleration therefore

`F = (73)(1.375)`

`F= 100.375N`

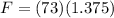
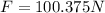
PART B) We will apply the same concept given but now we will change the time to 21s therefore:

`a = (V)/(t)\\a = (11)/(21)\\a = 0.5238`

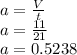
Now the force

`F = (73)(0.5238)`

`F = 38.23N`