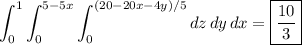Question

DOES ANYBODY KNOW HOW TO SOLVE THIS????

Find the volume of the given solid region in the first octant bounded by the plane 20x+4y+5z=20 and the coordinate​ planes, using triple integrals.


Complete the triple integral below used to find the volume of the given solid region. Note the order of integration dz dy dx.


The lower limits for all three are 0

Answer 1

You can find the intercepts of the plane with the three axes:

y = z = 0 ⇒ 20x = 20 ⇒ x = 1

x = z = 0 ⇒ 4y = 20 ⇒ y = 5

x = y = 0 ⇒ 5z = 20 ⇒ z = 4

which is to say, the plane has intercepts (1, 0, 0), (0, 5, 0), and (0, 0, 4).

For any point in the region, the z-coordinate will be bounded below by the plane z = 0 and above by the given plane z = (20 - 20x - 4y)/5.

Now shift the focus to the "shadow" of the given plane in the x-y plane. It's a triangular region in which the y-coordinate of any point in the "shadow" is bounded below by the line y = 0 and above by the line y = (20 - 20x)/4 = 5 - 5x.

Lastly, the x-coordinate is simply bounded between 0 and 1.

So, the volume of this region is

`\displaystyle \int_0^1 \int_0^(5-5x) \int_0^((20-20x-4y)/5) dz \, dy \, dx = \boxed{\frac{10}3}`