Answer:
The value of x , y for given linear equation using elimination is
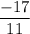 ,
,
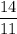 .
.
Explanation:
Given as :
The two linear equation are
-2 x + 7 y = 12 .............A
3 x + 6 y = 3 .............B
Solving the equation using elimination method
Now, multiply the equation A by 3
i.e 3 × ( - 2 x + 7 y ) = 3 × 12
Or, - 6 x + 21 y = 36 .......C
Again
multiply the equation B by 2
i.e 2 × ( 3 x + 6 y ) = 2 × 3
Or, 6 x + 12 y = 6 .....D
Now, Solving equation C an D
( - 6 x + 21 y ) + ( 6 x + 12 y ) = 36 + 6
Or , ( - 6 x + 6 x ) + ( 21 y + 12 y ) = 42
Or, (0) + (33 y ) = 42
Or, 33 y = 42
∴ y =
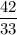
dividing numerator and denominator by 3
i.e y =
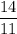
So, The value of y =
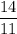
Now, Put the value of y into eq C
∵ - 6 x + 21 y = 36
Or, - 6 x + 21 ×
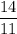 = 36
= 36
Or, - 6 x +
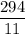 = 36
= 36
Or, - 6 x = 36 -
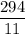
Or, - 6 x =
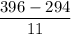
Or, - 6 x =
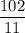
∴ x =
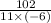
i.e x =
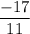
So, The value of x =
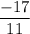
Hence, The value of x , y for given linear equation using elimination is
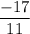 ,
,
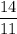 . Answer
. Answer