Question

I- A 2 Kilogram block situated on arough incline is

connectedto a light spring having a force constant of 100N/m. The
block isreleased from rest when the spring is un-stretched and the
pulleyis frictionless. the block moves 20 cm down the incline
beforecoming to rest. Find the coefficient of Kinetic friction
betweenthe block and the incline.
II- A 6 Kg block moving to the right with a velocity of
2m/scollides head-on with a 4 Kg block moving to the left with
avelocity of 3m/s.
a) if the collision is completely elastic, find the
finalvelocity of the blocks.
b)- if the collision is completely inelastic, find the
finalvelocity of the blocks.

Answer 1

Step-by-step explanation:

It is given that,

Mass of the block, m = 2 kg

Force constant of the spring, k = 100 N/m

Distance moved by the block down the incline before coming to rest is 20 cm or 0.02 m

(i) We need to find the coefficient of Kinetic friction between the block and the incline. It can be solved using the work energy theorem. The attached figure shows the whole scenario.

The work on the block during its slide is due to the force of friction and the gravity. The potential energy of the block is contributed due to the potential energy of the block.

`W=\Delta K+\Delta P`

`-F_fd=(K_f-K_i)+(P_(gf)-P_(gi))+(P_(sf)-P_(si))`

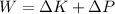
Where

`F_f` is the frictional force

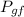`P_(gf)` is the final gravitational potential energy

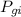`P_(gi)` is the initial gravitational potential energy

`P_(sf)` is the final spring potential energy

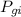`P_(gi)` is the initial gravitational potential energy

So,

`-\mu F_Nd=(0-0)+(-mgd\ sin\theta-0)+((1)/(2)kd^2-0)`

`\mu mgcos\theta=mg\ sin\theta-(1)/(2)kd^2`

`\mu=(mg\ sin\theta-(1/2)kd)/(mg\ cos\theta)`

`\mu=(2* 9.8* sin(37)-(1/2)100* 0.2)/(2* 9.8* cos(37))`

`\mu=0.1147`

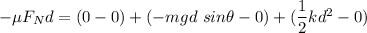
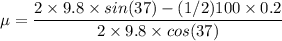
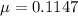
or

`\mu=0.115`

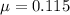
So, the coefficient of Kinetic friction between the block and the incline is 0.115.

(ii) The mass of the first block,
`m_1=6\ kg`

Mass of the second block,
`m_2=4\ kg`

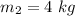
Speed of the first block,
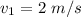`v_1=2\ m/s` (towards right)

Speed of the second block,
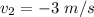`v_2=-3\ m/s` (towards left)

If the collision is completely elastic, both blocks will interchange their speeds such that the final speed of the first block is 3 m/s towards left and the final speed of the second block is 2 m/s towards right.

If the collision is completely inelastic, they will move with a common velocity after the collision. It is calculated using conservation of linear momentum as :

`m_1v_1+m_2v_2=(m_1+m_2)V`

`V=(m_1v_1+m_2v_2)/((m_1+m_2))`

`V=(6* 2+4* (-3))/((6+4))`

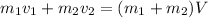
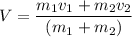
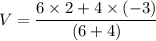
V = 0

So, if the collision is completely inelastic, they both stops such that their common velocity is equal to 0.

Hence, this is the required solution.