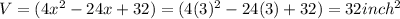Question

A piece of cardboard is twice as long as it is wide. It is to be made into a box with an open top by cutting 2-inch squares from each corner and folding up the sides. Let x represent the width of the original piece of cardboard. Determine a function ????(x) that represents the volume of the box. Determine the maximum Volume of the box.

Answer 1

A function that represents the volume of the box:

`V(x)=(4x^2-24x+32)`

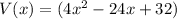
The maximum Volume of the box is
`32 inch^2`.

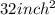Explanation:

Width of the card board= b = x

Length of the card board = l = 2x

Squares with sides of length x are cut out of each corner of a rectangular cardboard to form a box.

Now, length of the box = L = 2x - 4

Breadth of the box ,B= x - 4

Height of the box ,H= 2 inches

Volume of the box ,V= L × B × H =
`(2x-4)(x-4)2=(4x^2-24x+32)`

`V(x)=(4x^2-24x+32)`

`(dV)/(dx)=((2x-4)(x-4)2)/(dx)`

`(dV)/(dx)=(d(4x^2-24x+32))/(dx)`

`(dV)/(dx)=8x-24`

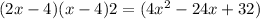
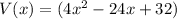
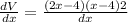
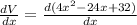
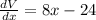
Putting ,
`(dV)/(dx)=0`

`0=8x-24`

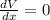
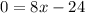
x = 3 inches

The maximum Volume of the box:

`V = (4x^2-24x+32)=(4(3)^2-24(3)+32)=32 inch^2`