Question

12. A research study was conducted to estimate the number of white perch (a type of fish) in a Midwestern lake. 300 perch were captured and tagged. After they were tagged, the perch

were released back into the lake. A scientist involved in the research estimates there are 1,000 perch in this lake. Several days after tagging and releasing the fish, the scientist caught 50
perch of which 20 were tagged. If this scientist’s estimate about the number of fish in the lake is correct, do you think it was likely to get 20 perch out of 50 with a tag? Explain your answer.

Answer 1

If the scientist’s estimate about the number of fish in the lake is correct, then it is 44% likely to get 20 perch out of 50 with a tag.

Explanation:

Let p be the proportion of tagged white perch in the Midwestern lake.

Scientist's claim is that p=
`(300)/(1000) =0.30`

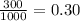
Let's test this hypothesis as:

• 
  `H_(0):` p=0.30

• 
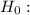  `H_(a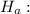):` p≠0.30

P-value of the test statistic will give the likelihood of getting 20 perch out of 50 with a tag if the scientist's estimate (
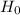`H_(0)`) is true.

Test statistic can be calculated using the equation

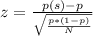`z=\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of white perch (
  `(20)/(50) =0.25`)

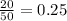• p is the proportion assumed under null hypothesis. (0.30)

• N is the sample size (50)

Then
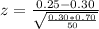`z=\frac{0.25-0.30}{\sqrt{(0.30*0.70)/(50) } }`≈ -0.77

Two tailed p-value of the test statistic is ≈ 0.44

Thus if the scientist’s estimate about the number of fish in the lake is correct, (p=0.30) then it is 44% likely to get 20 perch out of 50 with a tag.