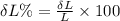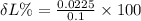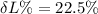Question

A brass cube, 10 cm on a side, is raised in temperature

by200C.
The coefficient of volume expansion ofbrass is
57x10-6/C.
By what percentage is anyone of the 10-cm edges increased
inlength?

Answer 1

`\delta L\%=22.5\%`

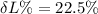
Step-by-step explanation:

Assuming that the thermal expansion of brass cube occurs isotropically (i.e. equal in all the directions).

Given:

• length of the cube,
  `l=10\ cm=0.1\ m`

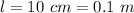
• change in temperature of the cube,
  `\Deta T=200\^(\circ)C`

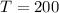
• coefficient of volume expansion,
  `\beta=57* 10^(-6)\ ^(\circ)C^(-1)`

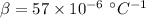
Hence volume of the cube:

`V=10^(-3)\ m^3`

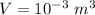
Now the volume of the cube after expansion:

`\delta V=V.\beta.\Delta T`

`\delta V=10^(-3)* 57* 10^(-6)* 200`

`\delta V=1.14* 10^(-5)\ m^3`

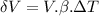
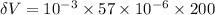
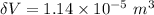
Therefore,

`\delta L=0.0225\ m`

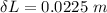
Now the percentage change in the edges of the cube:

`\delta L\%=(\delta L)/(L) * 100`

`\delta L\%=(0.0225)/(0.1) * 100`

`\delta L\%=22.5\%`