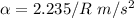Question

A hoop and a solid disc are relased from rest

atthe top of an incline and allowed to roll down the incline
withoutslipping.
Which is correct?
Estimate the angular acceleration of a
smallpebble stuck to a bicyle tire as the bicycle accelerates from
restto 10 mph (4.47 m/s) in 2 seconds.

Answer 1

The Solid disk gets to the bottom first. This is because the solid disk has a smaller moment of inertia compared to the hoop. As a result it rolls down the incline faster than the hoop. Although it has a smaller moment of inertia, it has a higher angular velocity.

Step-by-step explanation:

The steps for the solution to this problem can be found in the attachment below. Dynamics of rigid body has been applied in making a decision as to which body gets to the bottom first. Thank you.

Answer 2

1) The hoop and a solid disc rolling without slipping down an incline plane.

Their final velocities are proportional to their moment of inertia.

The condition for moment of inertia: v = ωR

We will use conservation of energy.

For the hoop:

`K_1 + U_1 = K_2 + U_2\\0 + m_hgh = (1)/(2)m_hv_h^2 + (1)/(2)I\omega_h^2 + 0`

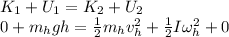
They are released from rest, so their initial kinetic energy is zero. And when they reach the bottom, their final potential energy is also zero.

The moment of inertia of a hoop is

`I_h = m_hR^2`

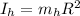
Let's continue with the energy equations:

`m_h gh = (1)/(2)m_hv_h^2 + (1)/(2)(m_hR^2)((v_h^2)/(R^2))\\m_hgh = (1)/(2)m_hv_h^2 + (1)/(2)m_hv_h^2\\m_hgh = m_hv_h^2\\v_h = √(gh)`

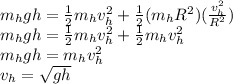
Similarly for the solid disk with a moment of inertia of (1/2)mR^2:

`K_1 + U_1 = K_2 + U_2\\m_dgh = (1)/(2)m_dv_d^2 + (1)/(2)I_d\omega_d^2\\m_dgh = (1)/(2)m_dv_d^2 + (1)/(2)((1)/(2)m_dR^2)((v_d^2)/(R^2))\\m_dgh = (1)/(2)m_dv_d^2 + (1)/(4)m_dv_d^2\\m_dgh = (3)/(4)m_dv_d^2\\v_d = \sqrt{(4gh)/(3)}`

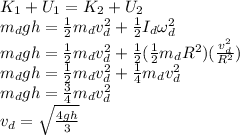
Comparing the final velocities, we can conclude that the solid disk reaches the bottom first.

2) The angular acceleration of the pebble is equal to the angular acceleration of the tire, since they stuck together. We can deduce the angular acceleration of the tire from the linear acceleration of the bicycle.

The kinematics equations states that

`v = v_0 + at\\4.47 = 0 + 2a\\a = 2.235 ~m/s^2`

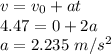
where a is the linear acceleration.

The relation with the angular and linear acceleration is

`a = \alpha R`

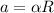
where R is the radius of the tire. Since it is not given in the question, we will leave it as R.

The angular acceleration of the small pebble is

`\alpha = 2.235/R ~m/s^2`