Question

A small metal sphere weighs .28 N in air and has a volume of13

cm3. How much will its apparent weight be whencompletely
submerged in water?

Answer 1

To solve this problem we will start by considering how to calculate the apparent weight. On the sphere this will then be given that the real weight is the sum of the apparent weight and the Buoyant Force. Therefore we will have to

`W_T = W_A + F_B`

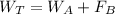
Here

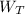`W_T`= True Weight

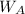`W_A`= Apparent Weight

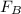`F_B`= Buoyant Force

If we seek to find the apparent weight we will have to,

`W_A = W_T-F_B`

`W_A = 0.28N - V\rho g`

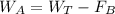
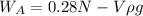
Remember that

V = Volume (Volume Sphere)

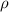`\rho`= Density (At this case water density)

g = Gravitational acceleration

`W_A = 0.28N - (13*10^(-6)m^3)(1000kg/m^3)(9.8)`

`W_A = 0.1526N`

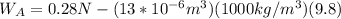
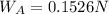
Therefore the apparent weight will be 0.1526N