Question

12. Using the value of 0.538 for the proportion of those surveyed who said they exercise at least 30 minutes three or more days a week in the most recent poll, calculate the margin

of error. How does your margin of error compare to the value reported by Gallup?

Answer 1

`ME=1.96\sqrt{(0.538 (1-0.538))/(15235)}=0.00792`

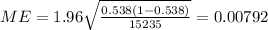
The margin of error on this case is approximated
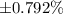`\pm 0.792\%` who is very clos to the +1% reported by the Gallup.

Explanation:

Assuming this previous info : "Results are based on telephone interview conducted as part of the Gallup-Healthways Well-Being Index survey June 1–30,2013, with a random sample of 15,235 adults, aged 18 and older, living in all 50 U.S. states and the District of Columbia.

For results based on the total sample of national adults, one can say with 95% confidence that the maximum margin of sampling error is ±1 percentage point."

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

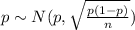
Solution to the problem

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 95% of confidence, our significance level would be given by
`\alpha=1-0.95=0.05` and
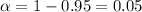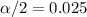`\alpha/2 =0.025`. And the critical value would be given by:

`z_(\alpha/2)=-1.96, z_(1-\alpha/2)=1.96`

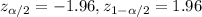
The estimated proportion on this case is
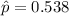`\hat p =0.538` and n =15235, the margin of error is given by:

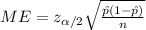`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

And if we replace we got:

`ME=1.96\sqrt{(0.538 (1-0.538))/(15235)}=0.00792`

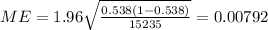
The margin of error on this case is approximated
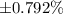`\pm 0.792\%` who is very clos to the +1% reported by the Gallup.