Question

Starting from rest, a 2-m-long pendulum swings from an angleof

12.8degrees. Of the choices below, which is closest to its speedat
the bottom position, where the angle is 0 degrees?
(Use sin 12.8degrees=0.22, cos 12.8degrees=0.975,
andg=10m/s^2)
A.) 100m/s
B.) 0.1m/s
C.) 10m/s
D.) 1m/s
E.) It is not possibel to naswer this question wihtout
knowingthe amss of the pendulum bob.
Answer and explanation would be great. If you do not
know,please do not answer.

Answer 1

D.) 1m/s

Step-by-step explanation:

Assume the initial angle of the swing is 12.8 degree with respect to the vertical. We can calculate the vertical distance from this initial point to the lowest point by first calculate the vertical distance from this point the the pivot point:

`L_1 = L*cos(12.8) = 2*0.975 = 1.95 m`

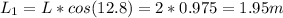
where L is the pendulum length

The vertical distance from the lowest point to the pivot point
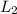`L_2` is the pendulum length 2m

this means the vertical distance from this initial point to the lowest point is simply:

`L_3 = L_2 - L_1 = 2 - 1.95 = 0.05 m`

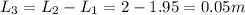
As the pendulum travel (vertically) from the initial point to the bottom point, its potential energy is converted to kinetic energy:

`E_p = E_k`

`mgh = mv^2/2`

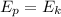
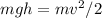
where m is the mass of the pendulum, g = 10 m/s2 is the constant gravitational acceleration, h = 0.05 is the vertical it travels, v is the pendulum velocity at the bottom, which we are trying to solve for.

The m on both sides of the equation cancel out

`v^2 = 2gh = 2*10*0.05 = 1`

`v = √(1) = 1 m/s`

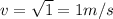
so D is the correct answer