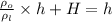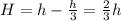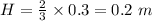Answer:
Step-by-step explanation:
Given
length of cubical box
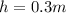
If density of object
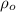 and density of lake liquid
and density of lake liquid
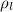
when it is in equilibrium one-third of its height
Buoyancy force will be equal to weight of cubical box
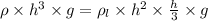
therefore
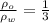
When water start Pouring in it then height of liquid at which box started to sink
Let H be that height
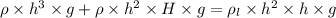
cancel out the common terms and divide by density of lake