Question

A simple harmonic oscillator has amplitude 0.76 m and

period2.9 sec. What is the maximum acceleration?

Answer 1

`(d^(2)x)/(dt^(2))=1.65(m/s^(2))`.

Step-by-step explanation:

To solve this problem we are going to consider the particle to be moving along the x axis and we are also going use the differential equation of the simple harmonic oscillator:

`(d^(2)x)/(dt^(2))+\omega^(2)x=0`,

`(d^(2)x)/(dt^(2))=-\omega^(2)x`,

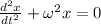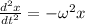where
`x` is the displacement along the x axis from the equilibrium point, and
`\omega` is the angular frecuency.

We know that
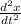`(d^(2)x)/(dt^(2))` is the acceleration of the particle and that the angular frecuancy depends on the period:

`\omega=(2\pi)/(T)`.

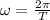By substitution we get

`(d^(2)x)/(dt^(2))=-(2\pi)/(T)x`.

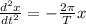We get the maximum and minimum acceleration at a displacement equals the
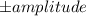`\pm amplitude`. Since we are moving along the x-axis, we get the maximum acceleration at
`x=-0.76m`.

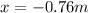So

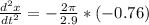`(d^(2)x)/(dt^(2))=-(2\pi)/(2.9)*(-0.76)`,

`(d^(2)x)/(dt^(2))=1.65(m/s^(2))`.