Question

Q.By the method of dimensional analysis derive the

relation:S=ut+1/2at2 where the letters have their
usualmeanings.
Q. Why is it so that two identical spheres of which one
issolid and other hollow take diffrent times to descend an
inclinedplane.?

Answer 1

LHS=RHS=[L]

Two identical spheres of which one is solid and other hollow take different times to descend an inclined plane because of their different mass distribution about the center of rotation.

Step-by-step explanation:

Given mathematical expression:

where: dimension:

s = displacement length
`[L]`

u = initial velocity
`[L.T^(-1)]`

t = time
`[T]`

a = acceleration
`[L.T^(-2)]`

now using dimensional analysis:

`LHS=[L]`

and

`RHS=[L.T^(-1)]* [T]+[L.T^(-2)]* [T]^2`

we know that the ratio and constants have no dimension.

`\Rightarrow RHS=[L]`

∵LHS=RHS

As we know that only similar dimensions can be added or subtracted therefore we get a correct conclusion.

However we can deduce the operators between the equations and can neither check for the validity of the constants. We can only check for the dimension of the terms involved.

2)

Two identical spheres of which one is solid and other hollow take different times to descend an inclined plane because of their different rolling motion.

we know that:

• the moment of inertia of a solid sphere is given as,
  `I=(2)/(5) m.R^2`

• the moment of inertia of a hollow sphere is given as,
  `I=(2)/(3) m.R^2`

Torque during the rolling would be given as:

`\tau=I.\alpha`

`\Rightarrow \alpha=(\tau)/(I)`

This indicates that the solid sphere will descend first when other parameters remain constant.

Answer 2

a) Using dimensional analysis we cannot derive the relation, But we can check the correctness of the formula.

`s = u t +(1)/(2)at^2`

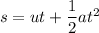
now, L H S

s = distance

dimension of distance = [M⁰L¹T⁰]

now, equation on the right hand side

R H S

u = speed

u = m/s

Dimension of speed = [M⁰L¹T⁻¹]

dimension of time

t = sec

Dimension of time = [M⁰L⁰T¹]

Dimension of 'ut' = [M⁰L¹T⁻¹][M⁰L⁰T¹]

= [M⁰L¹T⁰]

now, acceleration= a

a = m /s²

dimension of acceleration = [M⁰L¹T⁻²]

dimension of (at²) = [M⁰L¹T⁻²][M⁰L⁰T¹][M⁰L⁰T¹]

= [M⁰L¹T⁰]

hence, the dimension are balanced.

so, L H S = R H S

b) Moment of inertia of hollow sphere =
`(2)/(3)Mr^2`

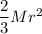
Moment of inertia of solid sphere =
`(2)/(5)Mr^2`

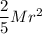
we know,

`\tau = I \alpha`

`\alpha=(\tau)/(I)`

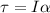
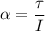
Torque is the force that causes rotation

If the same amount of torque is applied to both spheres the sphere with bigger moment of inertia would have smaller angular velocity.

Thus the solid sphere would accelerate more.