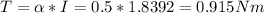Answer:
0.915 Nm
Step-by-step explanation:
1 revolution = 2π rad
We can use the following equation of motion to find out the acceleration acting on the disk
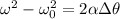
where
![\omega v = 2.5 rad/s is the final angular velocity of the disk, [tex]\omega_0](https://img.qammunity.org/2021/formulas/physics/college/o16v2l9x7xp7rmfl6oreze90c7fkdhl6wz.png) = 0 rad/s is the initial velocity of the can when it starts from rest,
= 0 rad/s is the initial velocity of the can when it starts from rest,
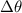 is the angular distance traveled,
is the angular distance traveled,
 is the angular acceleration of the disk, which we care looking for:
is the angular acceleration of the disk, which we care looking for:
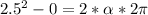
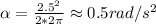
The moment of inertia of the solid disk is:
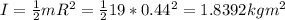
where m is the mass and R is the radius of the disk
The net torque applied is