Answer:
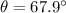 below the horizontal.
below the horizontal.
Step-by-step explanation:
This is a projectile motion problem. So we are going to use uniform motion and free-fall formulas.
Since what we want is the angle of the diver when hitting the water, we are going to search for the components of the final velocity and with them compute the angle.
For the free-fall part we know:
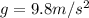 ,
,
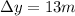 ,
,
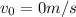 (remember that the initial velocity in the vertical component is zero because at the begining he only has horizontal velocity).
(remember that the initial velocity in the vertical component is zero because at the begining he only has horizontal velocity).
For the uniform motion part:
Notice that we already have the final velocity in the x coordinate (uniform motion means that the velocity is constant).
For the final velocity in y coordinate we are going to use:
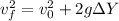 ,
,
since
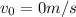 we get
we get
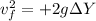 ,
,
![v_(f)=\sqrt[2]{2g\Delta Y}](https://img.qammunity.org/2021/formulas/physics/college/kxba4tt2vqo7rgkmvjuj6k2vcacnannhi8.png) ,
,
![v_(f)=\sqrt[2]{2(9.8)(13)}](https://img.qammunity.org/2021/formulas/physics/college/2aqsdiegaq18oh4m9eeka05w5gfb6r3aw2.png) ,
,
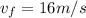 .
.
Now we can find the angle using the tangent function and the components of the final velocity. Remember that they are related as follow:
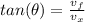 ,
,
where
 is the angle below the horizontal (the angle we are searching for).
is the angle below the horizontal (the angle we are searching for).
We have that
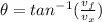
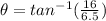
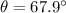 .
.