Question

Several guys went to eat lunch at Subway

and bought four cold drinks and seven
Subway sandwiches for $21.60. Joseph and
his date had two cold drinks and three
Subway sandwiches. If the sandwiches cost
twice as much as the cold drinks, how much
was Joseph's bill?
Write 2 systems of equations?????pleaseeee help???

Answer 1

Joseph's bill was $9.6.

Explanation:

Given:

Number of cold drinks = 4

Number of subway sandwiches = 7

Total cost of cold drinks and sandwiches = $21.60

The sandwiches cost twice as much as the cold drinks

To Find:

How much was Joseph's bill = ?

Solution:

Let the cost of one cold drink be x

The cost of sandwich be y

The sandwiches cost twice as much as the cold drinks

then

y = 2x--------------------------------------(1)

Now the total amount can be represented as

4x+7y =21.60-----------------------------(2)

Substituting (1) in (2)

4x+7(2x) =21.60

4x+14x =21.60

18x =21.60

`x = (21.60)/(18)`

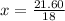
x = 1.2--------------------------------------(3)

The cost of one cold drink is $1.2

On substituting (3) in(1)

y = 2(1.2)

y = 2.4

The cost of one sandwich is $2.4

Now ,Joseph and his date had two cold drinks and three Subway sandwiches. So Joseph bill will be

=>
`( 2 * \text{ cost of one cold drink} )+ (3 * \text{ cost of one subway sandwich})`

=>
`(2 * 1.2) + (3 * 2.4)`

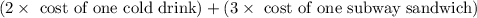
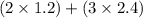
=>(2.4) + (7.2)

= 9.6