Answer:
A λ = 97.23 nm
, B) λ = 486.2 nm
, C) λ = 53326 nm
Step-by-step explanation:
With that problem let's use the Bohr model equation for the hydrogen atom
 = -k e² /2a₀ 1/n²
= -k e² /2a₀ 1/n²
For a transition between two states we have
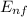 -
-
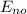 = -k e² /2a₀ (1/
= -k e² /2a₀ (1/
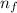 ² - 1 / n₀²)
² - 1 / n₀²)
Now this energy is given by the Planck equation
E = h f
And the speed of light is
c = λ f
Let's replace
h c / λ = - k e² /2a₀ (1 /
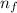 ² - 1 / no₀²)
² - 1 / no₀²)
1 / λ = - k e² /2a₀ hc (1 /
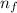 ² -1 / n₀²)
² -1 / n₀²)
Where the constants are the Rydberg constant
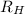 = 1.097 10⁷ m⁻¹
= 1.097 10⁷ m⁻¹
1 / λ =
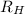 (1 / n₀² - 1 / nf²)
(1 / n₀² - 1 / nf²)
Now we can substitute the given values
Part A
Initial state n₀ = 1 to the final state
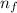 = 4
= 4
1 / λ = 1.097 10⁷ (1/1 - 1/4²)
1 / λ = 1.0284 10⁷ m⁻¹
λ = 9.723 10⁻⁸ m
We reduce to nm
λ = 9.723 10⁻⁸ m (10⁹ nm / 1m)
λ = 97.23 nm
Part B
Initial state n₀ = 2 final state
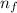 = 4
= 4
1 / λ = 1.097 10⁷ (1/2² - 1/4²)
1 / λ = 0.2056 10⁻⁷ m
λ = 486.2 nm
Part C
Initial state n₀ = 3
1 / λ = 1,097 10⁷ (1/3² - 1/4²)
1 / λ = 5.3326 10⁵ m⁻¹
λ = 5.3326 10-5 m
λ = 53326 nm