Question

A train consists of 50 cars, each of which has a mass 6.8

x10^3 kg. The train has an acceleration of +8.0 x 10^-2m/s^2.
Ignore friction and determine the tension in thecoupling a) between
the 30th and 31st cars and b) between the 49thand 50th cars.

Answer 1

The tension in the coupling between the 30th and 31st cars is 10,880 N. The tension in the coupling between the 49th and 50th cars is 5,440 N.

Step-by-step explanation:

To find the tension in the coupling between the 30th and 31st cars, we can use Newton's second law of motion, which states that the net force on an object is equal to the mass of the object multiplied by its acceleration. In this case, we can consider the two cars as a system, so the net force on the system is the tension in the coupling.

Using this equation, we have:

Tension = mass x acceleration = (mass of 30th car + mass of 31st car) x acceleration

Substituting the values, we get:

Tension =
`(2 x 6.8 x 10^3 kg) x (8.0 x 10^-2 m/s^2)`

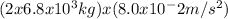
Therefore, the tension in the coupling between the 30th and 31st cars is 10,880 N.

To find the tension in the coupling between the 49th and 50th cars, we can follow the same approach. However, since it is the last car, it doesn't have any other car behind it. So, the tension in the coupling is equal to the force required to accelerate just that car.

Using the same equation as before, we have:

Tension = mass x acceleration = (mass of 50th car) x acceleration

Substituting the values, we get:

Tension =
`6.8 x 10^3 kg x 8.0 x 10^-2 m/s^2`

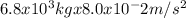
Therefore, the tension in the coupling between the 49th and 50th cars is 5,440 N.

Answer 2

Step-by-step explanation:

Given

mass of each car
`m=6.8* 10^3 kg`

acceleration of train
`a=8* 10^(-2) m/s^2`

Force required to pull this system

`F=50* ma`

For first car

`F-T{1-2}=ma`

`T_(1-2)=50ma-ma`

`T_(1-2)=49 ma`

for second car

`T_(1-2)-T_(2-3)=ma`

`T_(2-3)=49 ma-ma`

`T_(2-3)=48 ma`

this form a pattern of the form

`T_(n-(n+1))=(50-n)ma`

for (a)30 th and 31 st car tension

`T_(30-31)=(50-30) ma`

`T_(30-31)=20* 6.8* 10^(3)* 8* 10^(-2)`

`T_(30-31)=10,880\ N`

For 49 th and 50 th car

`T_(49-50)=(50-49) ma`

`T_(49-50)=544\ N`