Question

A new version of the Medical College Admissions Test (MCAT) was introduced in spring 2015 and is intended to shift the focus from what applicants know to how well they can use what they know. One result of the change is that the scale on which the exam is graded has been modified, with the total score of the four sections on the test ranging from 472 to 528. In spring 2015, the mean score was 500.0 with a standard deviation of 10.6.

What are the median and the first and third quartiles of the MCAT scores?

Median=
Q1(rounded to three decimal places)=
Q3(rounded to three decimal places)=
The IQR (interquartile range, rounded to three decimal places) =

Choose the interval that contains the central 80% of the MCAT scores.

a.491.096 to 508.904
b.472 to 528
c.480 to 520
d.486.432 to 513.568

Answer 1

• median=500

• Q1= 492.792

• Q3= 507.208

• IQR= 14.416

central 80% of the MCAT scores is 486.432 to 513.568

Explanation:

If we assume a normal distribution of the MCAT scores in spring 2015, then mean=median=500

first quartile Q1 is the first 25% boundary of the scores, thus

P(z<z*)=0.25 where z* is the z-score of Q1.

P(z<z*)=0.25 gives z*=-0.68

z-score of Q1 can be stated as follows:

`-0.68=(X-M)/(s)` where where

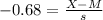• X is the Q1 score

• M is the mean MCAT score (500)

• s is the standard deviation (10.6)

Solving the equation for Q1 we get Q1= -0.68×10.6 + 500 ≈ 492.792

Similarly for third quartile Q3 z* is P(z<z*)=0.75 gives z*=0.68

That is Q3= 0.68×10.6 + 500 ≈ 507.208

IQR ( Interquartile Range) is IQR=Q3-Q1 = 507.208 - 492.792 = 14.416

for central 80% of the MCAT scores P(-z*<z<z*)=0.80 gives z*=1.28

that is upper bound = 1.28×10.6 + 500 ≈ 513.568

lower bound = -1.28×10.6 + 500 ≈ 486.432