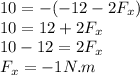Answer:
The question is incomplete, below is the complete question "A particle moves through an xyz coordinate system while a force acts on it. When the particle has the position vector r with arrow = (2.00 m)i hat − (3.00 m)j + (2.00 m)k, the force is F with arrow = Fxi hat + (7.00 N)j − (5.00 N)k and the corresponding torque about the origin is vector tau = (4 N · m)i hat + (10 N · m)j + (11N · m)k.
Determine Fx."
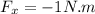
Step-by-step explanation:
We asked to determine the "x" component of the applied force. To do this, we need to write out the expression for the torque in the in vector representation.
torque=cross product of force and position . mathematically this can be express as

Where
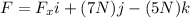 and the position vector
and the position vector
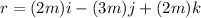
using the determinant method to expand the cross product in order to determine the torque we have
![\left[\begin{array}{ccc}i&j&k\\2&-3&2\\ F_(x) &7&-5\end{array}\right]\\\\](https://img.qammunity.org/2021/formulas/physics/college/shhd9d9n5t98g3lncsiiluqfvj9hmdl936.png)
by expanding we arrive at
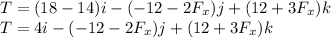
since we have determine the vector value of the toque, we now compare with the torque value given in the question
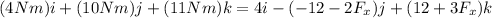
if we directly compare the j coordinate we have