Question

A 4.0kg block is suspended from a spring with force constant

of500N/m. A 50g bullet
is fired into the block from directly below with a speed of
150m/sand is imbedded in the
block. (a) Find the amplitude of the resulting simple
harmonicmotion. (b) What fraction
of the original kinetic energy of the bullet appears as
mechanicalenergy in the harmonic
oscillation?

Answer 1

(a) Amplitude of the motion is 0.184 m.

(b) 0.285 of the original kinetic energy appears as the mechanical energy in the harmonic oscillation.

Step-by-step explanation:

(a) First we will use the conservation of linear momentum to find the velocity of the combined objects.

`P_1 = P_2\\mv_1 = (M + m) v_2\\0.05*150 = (4 + 0.05)v_2\\v_2 = 1.85~m/s`

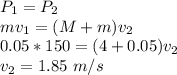
Before the collision, the spring is in equilibrium, so it is stretched by the amount of x.

`kx = Mg\\x = (Mg)/(k) = (4*9.8)/(500) = 0.0784~m`

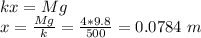
Just after the collision, the motion starts from this position.

The simple harmonic motion equation is

`x(t) = A\cos(\omega t + \phi)\\v(t) = (dx(t))/(dt) = -\omega A\sin(\omega t + \phi)`

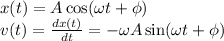
ω is the angular frequency, and given as

`\omega = \sqrt{(k)/(m)} = \sqrt{(500)/(4.05)} = 11.11`

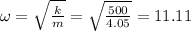
Φ is the phase angle and can be found by the initial conditions.

At t = 0 (Just after the collision);

`x(t=0) = 0.0784 = A\cos(\omega * (0) + \phi) = A\cos(\phi)\\v(t=0) = 1.85 = -(11.11)A\sin(\phi)\\\\\cos(\phi) = 0.0784/A\\A = -0.1665/\sin(\phi)\\\\\cos(\phi) = (0.0784)/(-(0.1665)/(\sin(\phi))) = 0.4709\sin(\phi)\\\cot(\phi) = 0.4709\\\phi = 64.7^\circ\\A = (0.1665)/(\sin(\phi)) = (0.1665)/(0.9044) =  0.184~m`

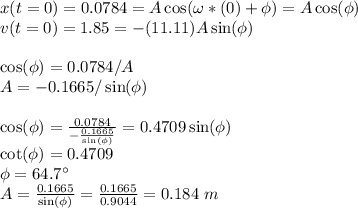
(b) The original kinetic energy is

`K_0 = (1)/(2)mv^2 = 562.5~J`

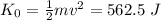
The mechanical energy of the simple harmonic motion is

`K + U = (1)/(2)(M+m)v_2^2 + (1)/(2)k_x^2 = (1)/(2)(4.05)(1.85)^2 + (1)/(2)500(0.0784)^2\\K+ U = 160.59~J`

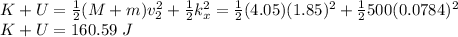
So 0.285 of the original kinetic energy appears as the mechanical energy in the harmonic oscillation. The rest of the original energy is converted to heat during the collision.