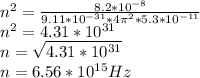Question

In the Bohr model of the hydrogen atom, an electron({rm mass};m=9.1; times 10^{ - 31;}{rm kg}) orbits a proton at a distance of 5.3 times 10^{ - 11;}{rm m}. The proton pulls on the electron with an electricforce of 8.2 times 10^{ - 8};{rm N}. How many revolutions per second does theelectron make?

Answer 1

n=6.56×10¹⁵Hz

Step-by-step explanation:

Given Data

Mass=9.1×10⁻³¹ kg

Radius distance=5.3×10⁻¹¹m

Electric Force=8.2×10⁻⁸N

To find

Revolutions per second

Solution

Let F be the force of attraction

let n be the number of revolutions per sec made by the electron around the nucleus then the centripetal force is given by

F=mω²r......................where ω=2π n

F=m4π²n²r...............eq(i)

as the values given where

Mass=9.1×10⁻³¹ kg

Radius distance=5.3×10⁻¹¹m

Electric Force=8.2×10⁻⁸N

we have to find n from eq(i)

n²=F/(m4π²r)

`n^(2) =(8.2*10^(-8) )/(9.11*10^(-31)* 4\pi^(2) *5.3*10^(-11)  )\\ n^(2)=4.31*10^(31)\\ n=\sqrt{4.31*10^(31)}\\ n=6.56*10^(15)Hz`