Answer:
a) The distribution is assymetric and on this case skewed to the right since we have the majority of the values on the left tail.
We can calculate the mean like this:
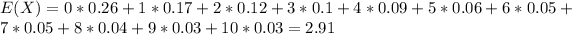
So we can conclude that the mean is between 2 and 3 cards. And most of the values are between 0 and 4 credit cards.
b) We have on this case that P(X=0) = 0.26 who represent the probability of no credit card. And the probability of having 7 or more cards is equal to P(X=7)+P(X=8) +P(X=9) +P(X=10)=0.05+0.04+0.03+0.03=0.15. So then the probability of having 0 credit card is higher.
c) We have a rectangle with height 0.25 and the width is 1 so then the area would be:

d) The total area below the curve need's to be 1 since all the rectangles present width of 1 and the sum of all the heights is 1 so then the sum of all the areas is 1.
Explanation:
Assuming the distribution given on the figure attached.
a. Describe the distribution.
The distribution is assymetric and on this case skewed to the right since we have the majority of the values on the left tail.
We can calculate the mean like this:
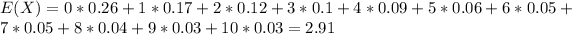
So we can conclude that the mean is between 2 and 3 cards. And most of the values are between 0 and 4 credit cards.
b. Is a randomly selected adult more likely to have 0 credit cards or 7 or more credit cards?
We have on this case that P(X=0) = 0.26 who represent the probability of no credit card. And the probability of having 7 or more cards is equal to P(X=7)+P(X=8) +P(X=9) +P(X=10)=0.05+0.04+0.03+0.03=0.15. So then the probability of having 0 credit card is higher.
c. Find the area of the bar representing 0 credit cards.
We have a rectangle with height 0.25 and the width is 1 so then the area would be:

d. What is the area of all of the bars in the histogram? Explain your reasoning.
The total area below the curve need's to be 1 since all the rectangles present width of 1 and the sum of all the heights is 1 so then the sum of all the areas is 1.