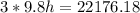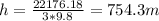Question

A solid disk has a mass of 162 kg and a radius of 1.30m. This

disk rotates about an axis through its center, like acompact discl
and has an angulaar speed of 18.0 rad/s. If allthe kinetic energy
of this disk were used to lift a 3.00 kg block,how high could the
block be lifted?

Answer 1

754.3 m

Step-by-step explanation:

The moment of inertia of the solid disk:

`I = mR^2/2`

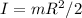
Where m is the disk mass and R is the radius of the disk.

`I = 162*1.3^2/2 = 136.89 kgm^2`

The angular kinetic energy of the disk is then:

`E_k = I\omega^2/2 = 136.89 * 18^2/2 = 22176.18 J`

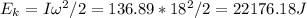
By law of energy conservation, this energy is converted to potential energy to pick up the 3kg block

let g = 9.8 m/s2

`E_p = m_bgh = 22176.18 J`

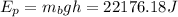
where
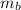`m_b` = 3 kg is the mass of block

`3*9.8h = 22176.18`

`h = (22176.18)/(3*9.8) = 754.3 m`