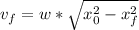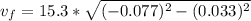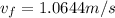Question

A horizontal spring is lying on a frictionless surface. Oneend

of the spring is attaches to a wall while the other end isconnected
to a movable object. The spring and object are compressedby 0.077
m, released from rest, and subsequently oscillate back andforth
with an angular frequency of 15.3 rad/s. What is the speed ofthe
object at the instant when the spring is stretched by0.033
m relative to its unstrained length?

Answer 1

`v_(f)=1.0644 m/s`

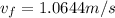
Step-by-step explanation:

According to law of conservation of energy:

Total initial Energy= Total Final Energy

`E_(0) = E_(f)`

`(1)/(2)*mv_(0) ^(2)+(1)/(2)*kx_(0) ^(2)=(1)/(2)*mv_(f) ^(2)+(1)/(2)*kx_(f) ^(2)`

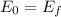
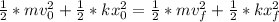
In above expression

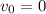`v_(0)=0` (System is initially at rest)

So above expression will become:

`(1)/(2)*kx_(0) ^(2)=(1)/(2)*mv_(f) ^(2)+(1)/(2)*kx_(f) ^(2)`

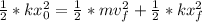
BY rearranging the above expression we will get final velocity/Speed:

`v_(f)=\sqrt{(k)/(m)}*\sqrt{x_(0) ^(2)-x_(f) ^(2)}`

`v_(f)=w*\sqrt{x_(0) ^(2)-x_(f) ^(2)}`

`v_(f)=15.3*\sqrt{(-0.077)^(2)-(0.033)^(2)}`

`v_(f)=1.0644 m/s`