Answer:
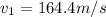
Step-by-step explanation:
The Bernoulli equation is:
 (1)
(1)
- P is pressure related to the fluid
- ρ is the density of the fluid (ρ(air)=1.23 kg/m³)
- v is the speed of the fluid
- h is the displacement from one position to the other
Now let's apply the equation (1), for our case:
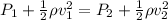 (2)
(2)
here we assume that h is the same in both cases so it canceled out.
- subscript 1 is related to the upper surface of the wings
- subscript 2 is related to the low surface of the wings
Solving the equation for v₁ we have:
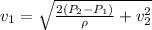 (3)
(3)
Now, we know that pressure P=F/A (force over area)
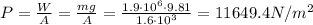 (4)
(4)
Combining (3) and (4), we can find v1.

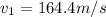
I hope it helps you!