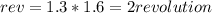Answer:
2 revolutions
Step-by-step explanation:
Assume that when she runs off the edge of the 8.3m high cliff, her vertical speed is 0. So gravitational acceleration g = 9.8m/s2 is the only thing that makes her fall down. So we can use the following equation of motion to calculate the time it takes for her to fall down:
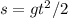
where s = 8.3 m is the distance that she falls, t is the time it takes to fall, which is what we are looking for
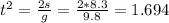

Since she rotates with an average angular speed of 1.6rev/s. The number of revolutions she would make within 1.3s is