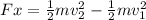Question

How can you use the Work-Energy Theorem to prove Newton's
1stand 2nd laws?

Answer 1

Work-Energy Theorem is that the work done on an object is equal to the change in the kinetic energy of that object:

`W = \Delta K = K_2 - K_1 = (1)/(2)mv_2^2 - (1)/(2)mv_1^2\\ Fx = (1)/(2)m(v_2^2 - v_1^2)`

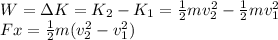
The relation between velocity and position is derived from the kinematics equations:

`v_2^2 = v_1^2 + 2ax\\x = (v_2^2 - v_1^2)/(2a)`

If we plug x into the work energy theorem, Newton's Second Law can be found:

`Fx = (1)/(2)m(v_2^2 - v_1^2)\\F(v_2^2 - v_1^2)/(2a) = (1)/(2)m(v_2^2 - v_1^2)\\F = ma`

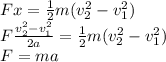
Newton's First Law is the law of inertia: If the net force on an object is zero, the acceleration of the object is also zero.

If the acceleration of the object is zero the kinematics equation yields:

`v_2^2 = v_1^2 + 2ax = v_1^2 + 2*0*x = v_1^2\\v_2 = v_1`

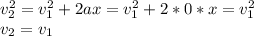
Then if we plug this into the work energy theorem

`Fx = (1)/(2)mv_2^2 - (1)/(2)mv_1^2`

`Fx = 0\\F_(net) = 0`