Answer:
a)
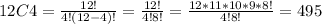 ways
ways
b)
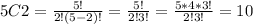 ways
ways
c)
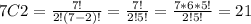 ways
ways
Explanation:
Combinatory means combination or arrangement of different elements.
If we have n total elements and we want to find in how many ways we can select x we can use this general formula:
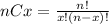
Where
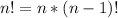
a. How many different ways can four pieces be selected from the 12 colored pieces?
For this case we have:
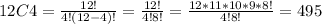 ways
ways
b. How many different ways can two orange pieces be selected from five orange pieces?
For this case we have:
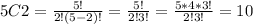 ways
ways
c. How many different ways can two brown pieces be selected from seven brown pieces?
For this case we have:
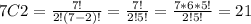 ways
ways